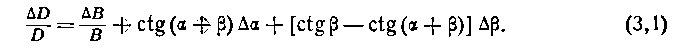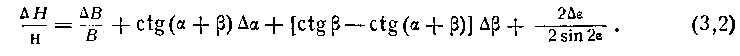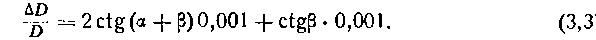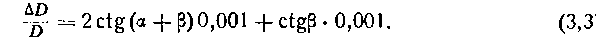ошибки Дальности по заданным ошибкам измерения базы и углов треугольника

В случае вычисления высоты Я по формуле (2,2) выражение для вычисления относительной ошибки в определении Н примет вид

Обычно ошибкой -g- можно пренебречь, так как разбивка базы на местности

может быть выполнена с высокой степенью точности; во всяком случае, точность до 0,25% не представляет каких-либо трудностей.

Ошибка в определении дальности от неточности измерения углов аир переменна и зависит от величины углов аир.

Допустим, что Да и Д(3 равны 0-01 (1 деление угломера), т. е. углы аир измерены с точностью до одной тысячной дистанции — точностью большинства угломерных приборов, принятых на вооружение; тогда формула (3,1) для вычисления До

величины примет вид

)

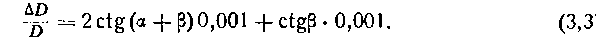В табл. 6 представлены значения первого и второго членов формулы для переменного значения углов аир

Таблица 6

a р	2ctg> + 3). 0,001	Р	ctg 8- 0,001
в градусах	в °/о	в градусах	в %
10	1,2	10	0,6
20	0,6	20	0,3
40	0,24	40	0,12
60	0,12	60	0,06
70	0,08	70	0,04
80	0,04	80	0,02
100	0,08
120	0,12
140	0,24
160	0,60
170	1,2

Табл. 6 показывает, что чем острее угол ~( = 180—(a-f-|5), т. е. чем более вытянут треугольник О АС к вершине, тем менее точно измеряется дистанция. Ошибка измерения вырастает также при очень острых углах (5, т. е. когда цель находится близко к направлению вдоль базы: в этом случае треугольник О АС слишком вытянут в сторону от базы.

Эти Два обстоятельства ставят ограничения для использования горизонтально-базного дальномера, именно: 1) нельзя допускать очень острые углы у, 2) нельзя измерять дистанцию под очень острыми углами р.

Если поставить требование, чтобы ошибки измерения Дистанции, происходящие от неточности угловых измерений, не превосходили 1°/₀, необходимо ограничить угол f, допустив измерение, только таких дистанций, для которых у>10°. Отсюда легко подсчитать приблизительно предельную дистанцию, которую можно еще измерять при данной базе.

Из формулы (2,1) получаем

№